

A variety of online introductory classes are available including semiconductor lasers, solid state physics, functional analysis and quantum optics. Please be aware that the current website is being rennovated and the online classes/notes will not be available until Fall 2020.

Semiconductor lasers
The online semiconductor lasers course presents the physical principles underlying the design, fabrication and operation of semiconductor lasers and LEDs. Special attention is given to the interaction of light with matter. The course applies basic EM theory, optics, quantum mechanics, solid state electronics and relevant math. It begins to explore the quantum nature of electromagnetic fields inlcuding coherent and squeezed states and the Wigner distribution. The course provides selected discussion and applications to CW and pulsed operation, mode locking, and gaseous and solid state lasers. The classes follow sections of the book titled Physics of Opto-electronics.
The typical first year graduate student and advanced undergraduate course (28 classes with approximately 1.5 hours each) covers a selection of topics including laser rate equations, the wave equations and transfer matrices, a brief summary of waveguiding, linear algebra, basic quantum theory especially time dependent perturbation theory and density operators, quantum dipole and Fermi’s golden rule, the Liouville equation and gain, Fermi’s golden rule approach to gain. Usually some material must be sacrificed between the Liouville equation and the Fermi’s golden rule approach for a 1 semester course. A follow-on short course (8-12 classes) can cover the introduction to quantum electro-dynamics (i.e., quantum optics) with prerequisite material on quantum representations and suggested material on noise from the beginning chapters.

Intro Quantum Theory and Solid State Physics
The course explores a wide range of concepts and tools needed to understand quantum theory, solid forms of matter and state-of-the-art electronic and optoelectronic devices. The course develops quantum theory from the start and then applies it to energy band theory, electrical transport, absorption and emission. The class follows the book titled Solid State and Quantum Theory for Opto-electronics.
The course devotes at least six or seven classes to the Hilbert spaces (discrete and continuous basis vectors, projection operators, orthonormal expansions, commutators, Hermitian and unitary operators, eigenvectors, and eigenvalues), at least six or seven classes to the introductory quantum theory (quantum wells, harmonic oscillator, time-independent perturbation theory, density operator), approximately four or five classes to phonons (direct and reciprocal lattices, dispersion curves and group velocity, and density of states), five or six classes to conduction and bands (quantum equation of continuity, effective mass, band diagrams, density of states, and, most importantly, the Bloch theorem), and at least four or five classes covering statistical mechanics and its application to carrier concentration (Lagrange multipliers, Boltzmann and Fermi distributions, Fermi functions, and diodes). More advanced classes can cover all of the book topics in the mathematics, the classical mechanics, quantum mechanical spin and angular momentum, propagators and the Feynman path integral, tensor mass, tight-binding, and k-p band theory. However, these additional topics are not necessary to read Physics of Optoelectronics as a follow-on course for semiconductor emitters and detectors, and as an introduction to quantum optics. The undergraduate reader (junior–senior) will find the Hilbert space and matrices accessible along with select sections in the quantum theory including the quantum well material, electron spin, harmonic oscillator, and the time-independent perturbation theory, as well as all of the material on phonons. The average undergraduate will be able to handle the conduction processes, scalar effective mass, Kronig-Penney model, and electron density of states.
Functional Analysis
The Functional Analysis course provides the foundations for advanced studies in Physics, Chemistry and especially engineering. This initial course covers selected topics in Complex Variables, Abstract Linear Algebra, Boundary Value Problems, Transform Theory, Probability Theory and Group Theory. This initial course emphasizes the linear algebra, boundary value problems and associated transform methods and special functions. The classes follow various books primarily the Functional Analysis books available for download on this website.
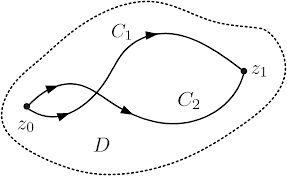
By way of more detail, the course presents linear functional systems from the viewpoint of Hilbert spaces, abstract operators, and intregral-differential operators. It explores the underlying connection between physical systems and mathematics, provides analytical techniques for modeling physical systems, and applies boundary value systems to engineering problems. The topics include Sturm-Liouville systems, series and integral representations, functions of operators, Green functions and propagators, introduction to group theory, calculus of variations, and special functions such as Legendre and Hermite polynomials, spherical harmonics and Bessel functions, and essential topics in complex variables including conformal mapping, branch cuts, and residues. The course develops the mathematics necessary for topics in solid state, quantum mechanics, and electrodynamics.
Intro. Quantum Opt.
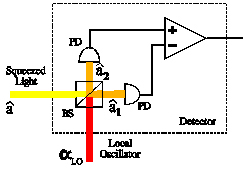
Quantum optics uses and extends the ideas of Quantum Electro-Dynamics (QED) which has often been called the most succesful and accurate physics theory. The electromagnetic field is expressed as an operator (second quantization) whereby the field amplitudes become operators. The various observed field properties are described by state vectors with Fock state expansions.
The course includes studies of coherent and the various squeezed states, wigner distributions, the methods and theory behind noise measurements, non-classical optical effects, matter-light interactions with various light states, quantum non-demolition experiments, Bell's Inequality, transfer functions of various optical components.